Because…why not?
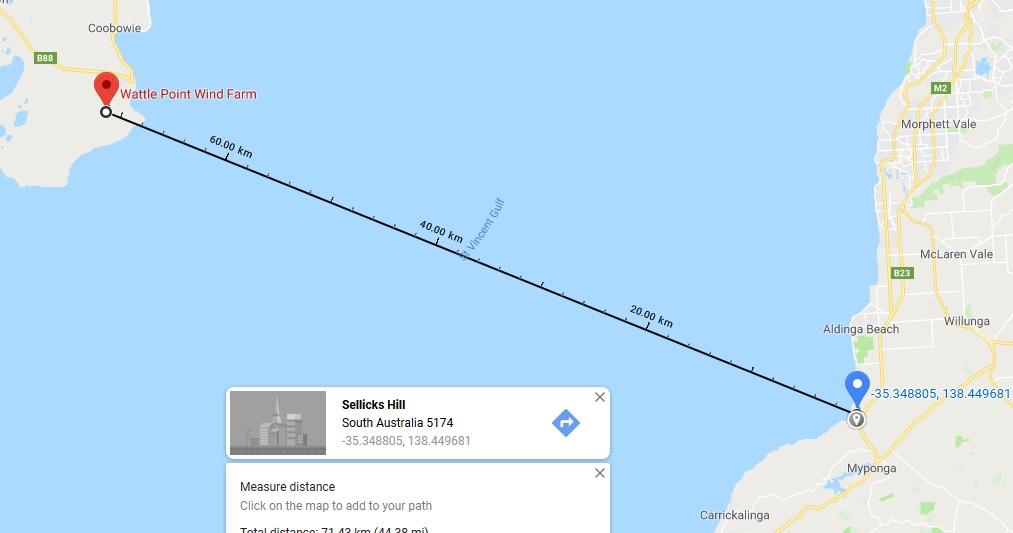
Last weekend we had a little getaway to Sellicks Beach, and at sunset I decided to head up to the Nan Hai Pu Tuo Temple and see if I could catch a nice sunset photo. I didn’t love the locations I could get to easily (there are too many trees in the way), but I did notice that I could see something that looked like a windfarm on the horizon. I didn’t think much more of it at the time other than “that’s pretty far away!”.


When I was going through my photos from the trip I noticed the turbines again, and decided to check out how far away it was on a map. It’s about 70 km away. I did a quick search for a distance-to-the-horizon-calculator, and to have been able to see 70 km, I would have needed to be at about 400 metres above sea level. The point I was photographing is definitely not 400 mASL.
I fired off some pictures to friends, quipping that it was proof that the earth was flat – how else would I be able to see that far. What I was actually thinking (and actually tweeted) is “How good is refraction!“.
Then I wanted to know how far that refraction was bending the light, so that I could see the windfarm from behind the horizon, so I decided to sit down to do a bit of maths (hence the title of this post, and also the title of my new category).
I looked up the approximate radius of our fair Earth. It’s 6,371 km. Then I used this site to look up the approximate elevations of the Buddha and the windfarm. The ground at the windfarm is at around 20 metres. The Buddha is at about 140 metres. I figured a turbine was about 60 metres tall, and it looked like I could see about two thirds of them in the photo (remember – this is all a bit approximate and back-of-an-envelope), so I figured that 60 metres was a good approximation for the height of the windfarm end.
From there it was on to trigonometry, and I won’t type all that up here. Instead, here is the slightly messy calculation.
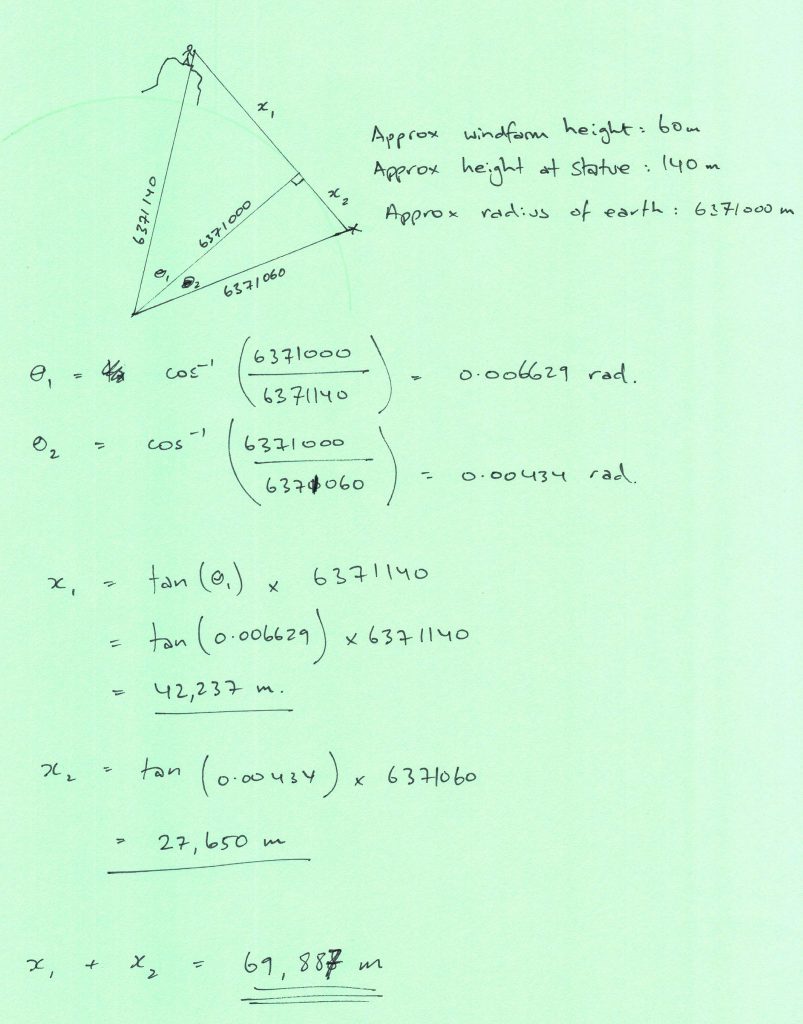
69.9 km!
The calculation of 400 metres elevation to see 70 km is assuming you’re looking at the ground at that height – basically assuming that you’re only calculating for x1.
I was amazed that it all worked out so neatly.
Shit yeah, maths!
And…well…take that, Flat Earth Society.